AI always does this shit.
“Do X thing”
“I don’t think that sounds like a good idea”
“You’re right! Don’t do X thing. Do Y thing instead”
it’s so fucking defeatist, but then again the alternative is the ai clowning me, which I actually experienced, NOT FUN EITHER.
Oh like when it just doubles, triples, and quadruples down? That is some of the funniest shit.
For context, bass guitar strings are tuned 3 octaves lower than that. The frequency of the A string is 55 Hz. You can’t even reach 220 Hz using the 12th fret on the highest (G) string. Tuning a bass A string to 8 times the frequency would require increasing its tension
almost 3 times64 times. The guitar bodyshouldwill not survive such forces but the string will snap long before you reach 110 Hz.Edit: got the quadratic formula the other way around
You can do the experiment on a non-bass guitar: “shorten” the high E string (330 Hz) by 5 frets to reach close to 440 Hz. It’s a chromatic scale and not a perfect fifth (error of +0.02 semitones) but that can be corrected without damage by holding the 5th fret and tuning the string to exactly 440 Hz. This shorter string will then react to the tuning fork as intended.
Or you can just use harmonics.
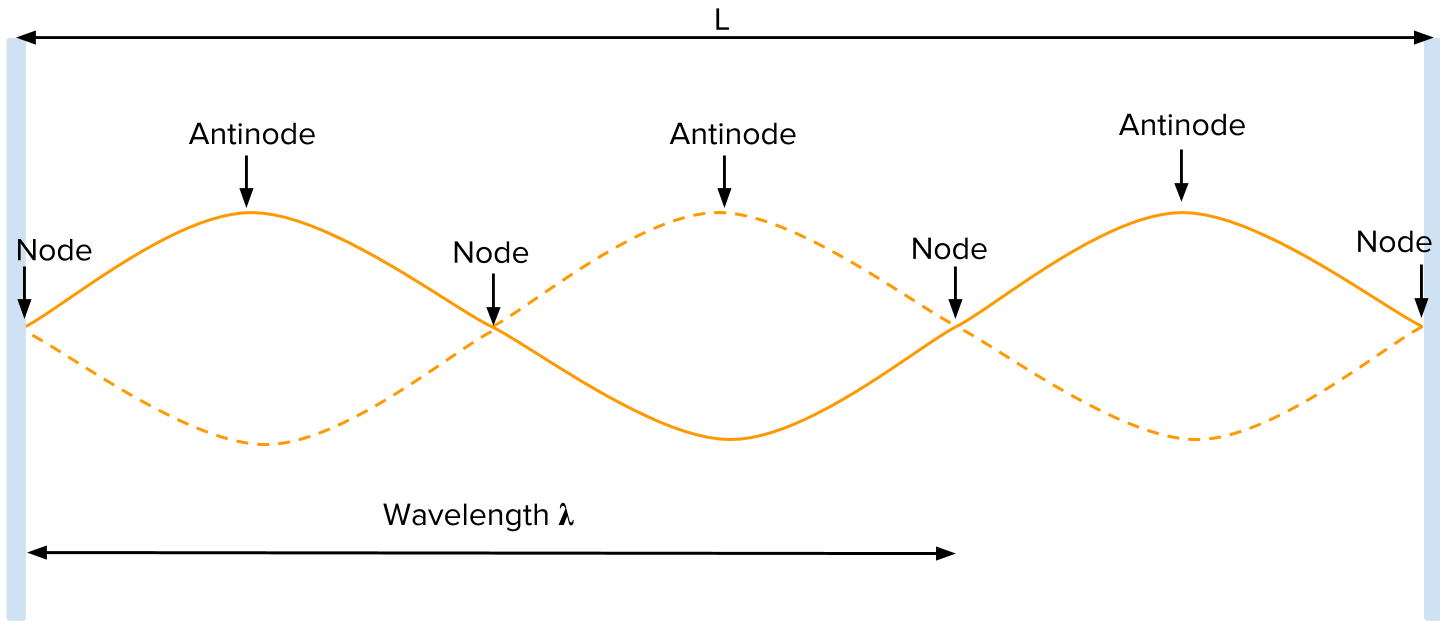
I think that would make a standing wave with a series of nodes/antinodes on the string, and how well it works would strongly depend on where the tuning fork is along the string. This has the potential to be more interesting but it’s not as easy. See my other comment for a table at which frequencies a standing wave occurs on the A1 string.
So the 12th fret is 1 octave up, 5th is 2 octaves, and just past the second fret is 3 octaves.
the 12th fret is 1 octave up
Yup. 12 semitones is 1 octave so A2 on the bass guitar’s A string. The frequency ratio to A1 is 2:1.
5th is 2 octaves
What? No. That’s 5 semitones or 500 cents from A1, which is D2, close to a perfect fourth from A1 (frequency ratio 4:3 or 498 cents).
Two octaves would be 24 semitones or 24 frets (not available on most fretted instruments) for a frequency ratio of 4:1, or A3.
just past the second fret is 3 octaves
No! The 2nd fret is 2 semitones or 200 cents above A1, which is B1, close to a major second from A1 (frequency ratio 9:8 or 196 cents).
3 octaves would be 36 semitones or 3600 cents for a frequency ratio of 8:1, or A4.
Sorry I mean that’s where the harmonics are.
For any harmonic, you first need to get a sound source of that frequency such as a tuning fork or speaker. It’s best to place the source where you expect an antinode to be. You can try to just pluck the string at that point but that will probably also produce a lots of harmonics you don’t want.
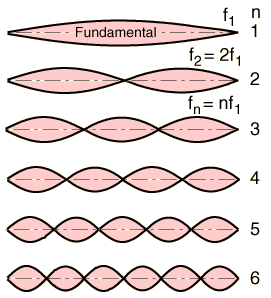
For the kth harmonic, there are k antinodes at (2i-1)/(2k) of the string length, where i≤k; i∈ℕ.
Fundamental (A1):
- ½ the string length (fret 12)
2nd harmonic (1 octave up, A2):
- ¾ the string length (fret 4.98)
- ¼ the string length
3rd harmonic (perfect fifth from A2 or approx. E3):
- ⅚ the string length (fret 3.15)
- ½ the string length (fret 12)
- ⅙ the string length
4th harmonic (2 octaves up, A3):
- ⅞ the string length (fret 2.32)
- ⅝ the string length (fret 8.14)
- ⅜ the string length
- ⅛ the string length
8th harmonic (4 octaves up, A4):
- 15/16 the string length (fret 1.12)
- 13/16 the string length (fret 3.59)
- 11/16 the string length (fret 6.49)
- 9/16 the string length (fret 9.96)
- 7/16 the string length
- 5/16 the string length
- 3/16 the string length
- 1/16 the string length
Using fractional frets is cumbersome because they are non-linear. You’re probably better off with a tape measure or ruler.
Yeah, you can’t tune your bass’s A string to a 440 Hz A. Lol
With that being said, the phenomenon the meme is referencing is called sympathetic resonance. It is not limited to matching intervals, but will resonate sympathetically at any frequency in the material’s harmonic scale. Any A will make any well-tuned A string resonate (or C#, D, E, or flat B/sharp Bb…), it just may be very low amplitude.
As Frozengyro@lemmy.world mentioned, you can have interesting results by using harmonics - tones that are a whole (k) multiple of the base frequency because then the string vibrates in a standing wave forming a series of k+1 nodes (including ends) and k antinodes equally spaced across its length. Such notes are:
Closest note Freq. Harm. Relation to A A1 55 Hz base (aka fundamental or open string frequency) A2 110 Hz 2nd octave above A1 E3 + 2 cents 165 Hz 3rd perfect fifth from A2 A3 220 Hz 4th octave above A2 C#4 - 14 cents 275 Hz 5th major third from A3 E4 + 2 cents 330 Hz 6th perfect fifth from A3 G4 - 31 cents 385 Hz 7th far from a note on the chromatic scale A4 440 Hz 8th octave above A3 B4 + 4 cents 495 Hz 9th major second from A4 C#5 - 14 cents 550 Hz 10th major third from A4 D#5 - 49 cents 605 Hz 11th very far from a note on the chromatic scale E5 + 2 cents 660 Hz 12th perfect fifth from A4 F5 + 41 cents 715 Hz 13th very far from a note on the chromatic scale G5 - 31 cents 770 Hz 14th far from a note on the chromatic scale G#5 - 12 cents 825 Hz 15th minor second below A5 A5 880 Hz 16th octave above A4 Frequencies and relations are exact, closest chromatic (piano) notes other than A are approximate, the deviation is expressed in whole cents (hundreths of semitones). Notes more than 20 cents off the chromatic scale will probably sound off so they are discouraged. You could continue forever but frequencies above that will have a very weak response.
Yes, you will get some resonance on non-integer multiples but way less.
Tbf they meant relative to the Stuttgart pitch. Humans would also refer to an orchestra tuning to concert pitch “A440.”
Y’know, you’re definitely right. But if Copilot were really useful it could have explained that.
I don’t think the AI meant anything.
“They” being the sources that the AI ingested to produce this output. AI is a word association machine, not a research tool. If people (“they”) call “tuning relative to A4=440Hz” “tune A to 440” AI will repeat it.
I’m just saying, while the OP is technically correct, one wouldn’t apply the same requirements on conversation with a human, which AI is built on.
LLMs mishmash from several sources. There isn’t a singular coherent “they”.
I understand, similar to “That’s what they say”, which is what I was idiomatically using “they” as in my original comment. I don’t really think it needs this much scrutiny.
I understand your point, but isn’t an orchestra ACTUALLY tuned to 440 (or 442 sometimes), because it’s usually a violin or oboe they’re tuning from? Like yeah, my bass isn’t going to be at 440, but the pitch I’m listening to while tuning is 440.
You’re right. Orchestras often tune to the oboe, because it can’t easily be tuned and usually stays in tune in conditions that would make other instruments go out of tune.
Cool - thanks for the sanity check.
