What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel’s incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham’s Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don’t even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 101010101010101010101010101010 (10s are stacked on each other)
- Σ(17) > Graham’s Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel’s incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham’s Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel’s incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach’s conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution
There are more ways to arrange a deck of 52 cards than there are atoms on Earth.
I feel this one is quite well known, but it’s still pretty cool.
An extension of that is that every time you shuffle a deck of cards there’s a high probability that that particular arrangement has never been seen in the history of mankind.
With the caveat that it’s not the first shuffle of a new deck. Since card decks come out of the factory in the same order, the probability that the first shuffle will result in an order that has been seen before is a little higher than on a deck that has already been shuffled.
Since a deck of cards can only be shuffled a finite number of times before they get all fucked up, the probability of deck arrangements is probably a long tail distribution
The most efficient way is not to shuffle them but to lay them all on a table, shift them around, and stack them again in arbitrary order.
assuming a perfect mechanical shuffle, I think the odds are near zero. humans don’t shuffle perfectly though!
perfect mechanical shuffle
What’s perfect in this context? It’s maybe a little counterintuitive because I’d think a perfect mechanical shuffle would be perfectly deterministic (assuming no mechanical failure of the device) so that it would be repeatable. Like, you would give it a seed number (about 67 digits evidently) and the mechanism would perform a series of interleaves completely determined by the seed. Then if you wanted a random order you would give the machine a true random seed (from your wall of lava lamps or whatever) and you’d get a deck with an order that is very likely to never have been seen before. And if you wanted to play a game with that particular deck order again you’d just put the same seed into the machine.
Perfect is the sense that you have perfect randomness. Like the Fisher-Yates shuffle.
In order to have a machine that can “pick” any possible shuffle by index (that’s all a seed really is, a partial index into the space of random numbers), you’d need a seed 223 bits long.
But you wouldn’t want perfect mechanical shuffles though because 8 perfect riffles will loop the deck back to it’s original order! The minor inaccuracies are what makes actual shuffling work.
I’d probably have the machine do it all electronically and then sort the physical deck to match, not sure you could control the entropy in a reliable way with actual paper cards otherwise.
For the uninitiated, the monty Hall problem is a good one.
Start with 3 closed doors, and an announcer who knows what’s behind each. The announcer says that behind 2 of the doors is a goat, and behind the third door is
a carstudent debt relief, but doesn’t tell you which door leads to which. They then let’s you pick a door, you get what’s behind the door. Before you open it, they open a different door than your choice and reveals a goat. Then the announcer says you are allowed to change your choice.So should you switch?
The answer turns out to be yes. 2/3rds of the time you are better off switching. But even famous mathematicians didn’t believe it at first.
I know the problem is easier to visualize if you increase the number of doors. Let’s say you start with 1000 doors, you choose one and the announcer opens 998 other doors with goats. In this way is evident you should switch because unless you were incredibly lucky to pick up the initial door with the prize between 1000, the other door will have it.
I now recall there was a numberphile with exactly that visualisation! It’s a clever visual
It really is, it’s how my probability class finally got me to understand why this solution is true.
This is so mind blowing to me, because I get what you’re saying logically, but my gut still tells me it’s a 50/50 chance.
But I think the reason it is true is because the other person didn’t choose the other 998 doors randomly. So if you chose any of the other 998 doors, it would still be between the door you chose and the winner, other than the 1/1000 chance that you chose right at the beginning.
I don’t find this more intuitive. It’s still one or the other door.
The point is, the odds don’t get recomputed after the other doors are opened. In effect you were offered two choices at the start: choose one door, or choose all of the other 999 doors.
This is the way to think about it.
The thing is, you pick the door totally randomly and since there are more goats, the chance to pick a goat is higher. That means there’s a 2/3 chance that the door you initially picked is a goat. The announcer picks the other goat with a 100% chance, which means the last remaining door most likely has the prize behind it
Edit: seems like this was already answered by someone else, but I didn’t see their comment due to federation delay. Sorry
Don’t be sorry, your comment was the first time I actually understood how it works. Like I understand the numbers, but I still didn’t get the problem, even when increasing the amount of doors. It was your explanation that made it actually click.
I think the problem is worded specifically to hide the fact that you’re creating two set of doors by picking a door, and that shrinking a set actually make each individual door in that set more likely to have the prize.
Think of it this way : You have 4 doors, 2 blue doors and 2 red doors. I tell you that there is 50% chance of the prize to be in either a blue or a red door. Now I get to remove a red door that is confirmed to not have the prize. If you had to chose, would you pick a blue door or a red door? Seems obvious now that the remaining red door is somehow a safer pick. This is kind of what is happening in the initial problem, but since the second ensemble is bigger to begin with (the two doors you did not pick), it sort of trick you into ignoring the fact that the ensemble shrank and that it made the remaining door more “valuable”, since the two ensembles are now of equal size, but only one ensemble shrank, and it was always at 2/3 odds of containing the prize.
The odds you picked the correct door at the start is 1/1000, that means there’s a 999/1000 chance it’s in one of the other 999 doors. If the man opens 998 doors and leaves one left then that door has 999/1000 chance of having the prize.
Same here, even after reading other explanations I don’t see how the odds are anything other than 50/50.
read up on the law of total probability. prob(car is behind door #1) = 1/3. monty opens door #3, shows you a goat. prob(car behind door #1) = 1/3, unchanged from before. prob(car is behind door #2) + prob(car behind door #1) = 1. therefore, prob(car is behind door #2) = 2/3.
Following that cascade, didn’t you just change the probability of door 2? It was 1/3 like the other two. Then you opened door three. Why would door two be 2/3 now? Door 2 changes for no disclosed reason, but door 1 doesn’t? Why does door 1 have a fixed probability when door 2 doesn’t?
No, you didn’t change the prob of #2. Prob(car behind 2) + prob(car behind 3) = 2/3. Monty shows you that prob(car behind 3) = 0.
This can also be understood through conditional probabilities, if that’s easier for you.
This is fantastic, thank you.
How do we even come up with such amazing problems right ? It’s fascinating.
But even famous mathematicians didn’t believe it at first.
They emphatically did not believe it at first. Marilyn vos Savant was flooded with about 10,000 letters after publishing the famous 1990 article, and had to write two followup articles to clarify the logic involved.
Oh that’s cool - I had heard one or two examples only. Is there some popular writeup of the story from Savant’s view?
I couldn’t tell you - I used the Wikipedia article to reference the specifics and I’m not sure where I first heard about the story. I just remember that the mathematics community dogpiled on her hard for some time and has since completely turned around to accept her answer as correct.
Also relevant - she did not invent the problem, but her article is considered by some to have been what popularized it.
I know it to be true, I’ve heard it dozens of times, but my dumb brain still refuses to accept the solution everytime. It’s kind of crazy really
To me, it makes sense because there was initially 2 chances out of 3 for the prize to be in the doors you did not pick. Revealing a door, exclusively on doors you did not pick, does not reset the odds of the whole problem, it is still more likely that the prize is in one of the door you did not pick, and a door was removed from that pool.
Imo, the key element here is that your own door cannot be revealed early, or else changing your choice would not matter, so it is never “tested”, and this ultimately make the other door more “vouched” for, statistically, and since you know that the door was more likely to be in the other set to begin with, well, might as well switch!
Let’s name the goats Alice and Bob. You pick at random between Alice, Bob, and the Car, each with 1/3 chance. Let’s examine each case.
-
Case 1: You picked Alice. Monty eliminates Bob. Switching wins. (1/3)
-
Case 2: You picked Bob. Monty eliminates Alice. Switching wins. (1/3)
-
Case 3: You picked the Car. Monty eliminates either Alice or Bob. You don’t know which, but it doesn’t matter-- switching loses. (1/3)
It comes down to the fact that Monty always eliminates a goat, which is why there is only one possibility in each of these (equally probable) cases.
From another point of view: Monty revealing a goat does not provide us any new information, because we know in advance that he must always do so. Hence our original odds of picking correctly (p=1/3) cannot change.
In the variant “Monty Fall” problem, where Monty opens a random door, we perform the same analysis:
- Case 1: You picked Alice. (1/3)
- Case 1a: Monty eliminates Bob. Switching wins. (1/2 of case 1, 1/6 overall)
- Case 1b: Monty eliminates the Car. Game over. (1/2 of case 1, 1/6 overall)
- Case 2: You picked Bob. (1/3)
- Case 2a: Monty eliminates Alice. Switching wins. (1/2 of case 2, 1/6 overall)
- Case 2b: Monty eliminates the Car. Game over. (1/2 of case 2, 1/6 overall)
- Case 3: You picked the Car. (1/3)
- Case 3a: Monty eliminates Alice. Switching loses. (1/2 of case 3, 1/6 overall)
- Case 3b: Monty eliminates Bob. Switching loses. (1/2 of case 3, 1/6 overall)
As you can see, there is now a chance that Monty reveals the car resulting in an instant game over-- a 1/3 chance, to be exact. If Monty just so happens to reveal a goat, we instantly know that cases 1b and 2b are impossible. (In this variant, Monty revealing a goat reveals new information!) Of the remaining (still equally probable!) cases, switching wins half the time.
-
like on paper the odds on your original door was 1/3 and the option door is 1/2, but in reality with the original information both doors were 1/3 and now with the new information both doors are 1/2.
Your original odds were 1/3, and this never changes since you don’t get any new information.
The key is that Monty always reveals a goat. No matter what you choose, even before you make your choice, you know Monty will reveal a goat. Therefore, when he does so, you learn nothing you didn’t already know.
Yes, you don’t actually have to switch. You could also throw a coin to decide to stay at the current door or to switch. By throwing a coin, you actually improved your chances of winning the price.
This is incorrect. The way the Monty Hall problem is formulated means staying at the current door has 1/3 chance of winning, and switching gives you 2/3 chance. Flipping a coin doesn’t change anything. I’m not going to give a long explanation on why this is true since there are plenty other explanations in other comments already.
This is a common misconception that switching is better because it improves your chances from 1/3 to 1/2, whereas it actually increases to 2/3.
This explanation really helped me make sense of it: Monty Hall Problem (best explanation) - Numberphile
It took me a while to wrap my head around this, but here’s how I finally got it:
There are three doors and one prize, so the odds of the prize being behind any particular door are 1/3. So let’s say you choose door #1. There’s a 1/3 chance that the prize is behind door #1 and, therefore, a 2/3 chance that the prize is behind either door #2 OR door #3.
Now here’s the catch. Monty opens door #2 and reveals that it does not contain the prize. The odds are the same as before – a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind either door #2 or door #3 – but now you know definitively that the prize isn’t behind door #2, so you can rule it out. Therefore, there’s a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind door #3. So you’ll be twice as likely to win the prize if you switch your choice from door #1 to door #3.
It’s a good one.
First, fuck you! I couldn’t sleep. The possibility to win the car when you change is the possibility of your first choice to be goat, which is 2/3, because you only win when your first choice is goat when you always change.
x1: you win
x2: you change
x3: you pick goat at first choice
P(x1|x2,x3)=1 P(x1)=1/2 P(x3)=2/3 P(x2)=1/2
P(x1|x2) =?
Chain theory of probability:
P(x1,x2,x3)=P(x3|x1,x2)P(x1|x2)P(x2)=P(x1|x2,x3)P(x2|x3)P(x3)
From Bayes theorem: P(x3|x1,x2)= P(x1|x2,x3)P(x2)/P(x1) =1
x2 and x3 are independent P(x2|x3)=P(x2)
P(x1| x2)=P(x3)=2/3 P(x2|x1)=P(x1|x2)P(x2)/P(X1)=P(x1|x2)
P(x1=1|x2=0) = 1- P(x1=1|x2=1) = 1\3 is the probability to win if u do not change.
Why do you have a P(x1) = 1/2 at the start? I’m not sure what x1 means if we don’t specify a strategy.
Just count the number of possibilities. If you change there there two possible first choices to win + if you do not change 1 possible choice to win = 3. If you change there is one possible first choice to lose + if you do not change there two possible first choices to lose=3 P(x1)=P(x1’) = 3/6
Goldbach’s Conjecture: Every even natural number > 2 is a sum of 2 prime numbers. Eg: 8=5+3, 20=13+7.
https://en.m.wikipedia.org/wiki/Goldbach’s_conjecture
Such a simple construct right? Notice the word “conjecture”. The above has been verified till 4x10^18 numbers BUT no one has been able to prove it mathematically till date! It’s one of the best known unsolved problems in mathematics.
Wtf !
How can you prove something in math when numbers are infinite? That number you gave if it works up to there we can call it proven no? I’m not sure I understand
There are many structures of proof. A simple one might be to prove a statement is true for all cases, by simply examining each case and demonstrating it, but as you point out this won’t be useful for proving statements about infinite cases.
Instead you could assume, for the sake of argument, that the statement is false, and show how this leads to a logical inconsistency, which is called proof by contradiction. For example, Georg Cantor used a proof by contradiction to demonstrate that the set of Natural Numbers (1,2,3,4…) are smaller than the set of Real Numbers (which includes the Naturals and all decimal numbers like pi and 69.6969696969…), and so there exist different “sizes” of infinity!
For a method explicitly concerned with proofs about infinite numbers of things, you can try Proof by Mathematical Induction. It’s a bit tricky to describe…
- First demonstrate that a statement is true in some 1st base case.
- Then demonstrate that if it holds true for the abstract Nth case, then it necessarily holds true for the (N+1)th case (by doing some clever rearranging of algebra terms or something)
- Therefore since it holds true for the 1th case, it must hold true for the (1+1)th case = the 2th case. And since it holds true for the 2th case it must hold true for the (2+1)=3th case. And so on ad infinitum.
Wikipedia says:
Mathematical induction can be informally illustrated by reference to the sequential effect of falling dominoes.
Bear in mind, in formal terms a “proof” is simply a list of true statements, that begin with axioms (which are true by default) and rules of inference that show how each line is derived from the line above.
Very cool and fascinating world of mathematics!
As you said, we have infinite numbers so the fact that something works till 4x10^18 doesn’t prove that it will work for all numbers. It will take only one counterexample to disprove this conjecture, even if it is found at 10^100. Because then we wouldn’t be able to say that “all” even numbers > 2 are a sum of 2 prime numbers.
So mathematicians strive for general proofs. You start with something like: Let n be any even number > 2. Now using the known axioms of mathematics, you need to prove that for every n, there always exists two prime numbers p,q such that n=p+q.
Would recommend watching the following short and simple video on the Pythagoras theorem, it’d make it perfectly clear how proofs work in mathematics. You know the theorem right? For any right angled triangle, the square of the hypotenuse is equal to the sum of squares of both the sides. Now we can verify this for billions of different right angled triangles but it wouldn’t make it a theorem. It is a theorem because we have proved it mathematically for the general case using other known axioms of mathematics.
That’s a really great question. The answer is that mathematicians keep their statements general when trying to prove things. Another commenter gave a bunch of examples as to different techniques a mathematician might use, but I think giving an example of a very simple general proof might make things more clear.
Say we wanted to prove that an even number plus 1 is an odd number. This is a fact that we all intuitively know is true, but how do we know it’s true? We haven’t tested every single even number in existence to see that itself plus 1 is odd, so how do we know it is true for all even numbers in existence?
The answer lies in the definitions for what is an even number and what is an odd number. We say that a number is even if it can be written in the form 2n, where n is some integer, and we say that a number is odd if it can be written as 2n+1. For any number in existence, we can tell if it’s even or odd by coming back to these formulas.
So let’s say we have some even number. Because we know it’s even, we know we can write it as 2n, where n is an integer. Adding 1 to it gives 2n+1. This is, by definition, an odd number. Because we didn’t restrict at the beginning which even number we started with, we proved the fact for all even numbers, in one fell swoop.
The four-color theorem is pretty cool.
You can take any map of anything and color it in using only four colors so that no adjacent “countries” are the same color. Often it can be done with three!
Maybe not the most mind blowing but it’s neat.
Thanks for the comment! It is cool and also pretty aesthetically pleasing!

Your map made me think how interesting US would be if there were 4 major political parties. Maybe no one will win the presidential election 🤔
What about a hypothetical country that is shaped like a donut, and the hole is filled with four small countries? One of the countries must have the color of one of its neighbors, no?

I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
In graph theory there are vertices and edges, two shapes are adjacent if and only if they share an edge, vertices are not relevant to adjacency. As long as all countries subscribe to graph theory we should be safe
The only problem with that it that it requires all countries to agree to something, and that seems to become harder and harder nowadays.
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should’ve been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You’re right. Bad example from my side. But imagine this scenario:

That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I’ve also used a dashed line to show the only difference in adjacency.
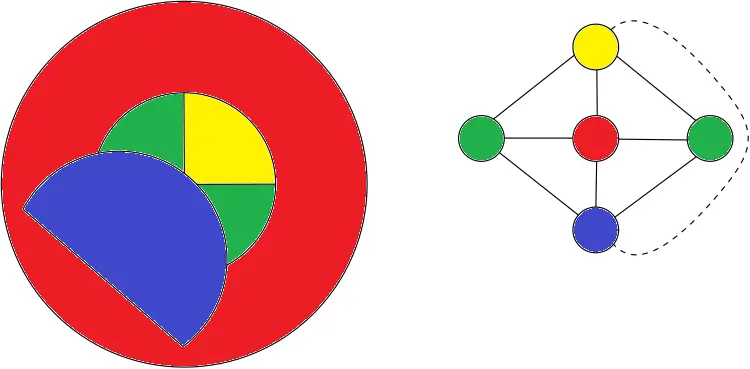
Oh wow, now I feel dumb. Thanks.
Make purple yellow and one of the reds purple.
…There is no purple though?
 Ok now do this one. What color is the donut country?
Ok now do this one. What color is the donut country?
Someone beat me to it, so I thought I’d also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.
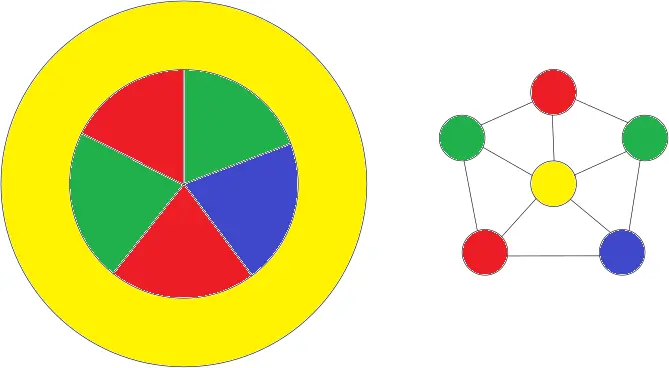
In that image, you could color yellow into purple since it’s not touching purple. Then, you could color the red inner piece to yellow, and have no red in the inner pieces.
There are some rules about the kind of map this applies to. One of them is “no countries inside other countries.”
Not true, see @BitSound’s comment.
It does have to be topologically planar (may not be the technical term), though. No donut worlds.
The regions need to be contiguous and intersect at a nontrivial boundary curve. This type of map can be identified uniquely with a planar graph by placing a vertex inside each region and drawing an edge from one point to another in each adjacent region through the bounding curve.
I see.
I read an interesting book about that once, will need to see if I can find the name of it.
EDIT - well, that was easier than expected!

Read the author as Robin Williams
Note you’ll need the regions to be connected (or allow yourself to color things differently if they are the same ‘country’ but disconnected). I forget if this causes problems for any world map.
I suspect that the Belgium-Netherlands border defies any mathematical description.
If you had a 3 dimensional map, would you need more colors to achieve the same results?
Edit: it was explained in your link. It looks like for surfaces in 3D space, this can’t be generalized.
this whole thread is the shit.
Isn’t the proof of this theorem like millions of pages long or something (proof done by a computer ) ? I mean how can you even be sure that it is correct ? There might be some error somewhere.
I came here to find some cool, mind-blowing facts about math and have instead confirmed that I’m not smart enough to have my mind blown. I am familiar with some of the words used by others in this thread, but not enough of them to understand, lol.
Same here! Great post but I’m out! lol
Nonsense! I can blow both your minds without a single proof or mathematical symbol, observe!
There are different sizes of infinity.
Think of integers, or whole numbers; 1, 2, 3, 4, 5 and so on. How many are there? Infinite, you can always add one to your previous number.
Now take odd numbers; 1, 3, 5, 7, and so on. How many are there? Again, infinite because you just add 2 to the previous odd number and get a new odd number.
Both of these are infinite, but the set of numbers containing odd numbers is by definition smaller than the set of numbers containing all integers, because it doesn’t have the even numbers.
But they are both still infinite.
Your fact is correct, but the mind-blowing thing about infinite sets is that they go against intuition.
Even if one might think that the number of odd numbers is strictly less than the number of all natural numbers, these two sets are in fact of the same size. With the mapping n |-> 2*n - 1 you can map each natural number to a different odd number and you get every odd number with this (such a function is called a bijection), so the sets are per definition of the same size.
To get really different “infinities”, compare the natural numbers to the real numbers. Here you can’t create a map which gets you all real numbers, so there are “more of them”.
I may be wrong or have misunderstood what you said but the sets of natural numbers and odd numbers have the same size/cardinality. If there exists a bijection between the two sets then they have the same size.
f(x) = 2x + 1 is such a bijection
For the same reason, N, Z and Q have the same cardinality. The fact that each one is included in the next ones doesn’t mean their size is different.
Agree. Uncountable infinities are much more mind blowing. It was an interesting journey realising first that everything like time and distance are continuous when learning math the then realising they’re not when learning physics.
Both of these are infinite, but the set of numbers containing odd numbers is by definition smaller than the set of numbers containing all integers, because it doesn’t have the even numbers.
This is provably false - the two sets are the same size. If you take the set of all integers, and then double each number and subtract one, you get the set of odd numbers. Since you haven’t removed or added any elements to the initial set, the two sets have the same size.
The size of this set was named Aleph-zero by Cantor.
There was a response I left in the main comment thread but I’m not sure if you will get the notification. I wanted to post it again so you see it
Response below
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here’s a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here’s a video from the best math teacher in the world.
That’s so cool! Thanks for the reply and the link.
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here’s a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here’s a video from the best math teacher in the world.
Thanks! I appreciate the response. I’ve seen some videos on 3blue1brown and I’ve really enjoyed them. I think if I were to go back and fill in all the blank spots in my math experience/education I would enjoy math quite a bit.
I don’t know why it appears here or why I feel this way, but picturing the box bouncing off the wall and back, losing energy, feels intuitively round to me.
For me, personally, it’s the divisible-by-three check. You know, the little shortcut you can do where you add up the individual digits of a number and if the resulting sum is divisible by three, then so is the original number.
That, to me, is black magic fuckery. Much like everything else in this thread I have no idea how it works, but unlike everything else in this thread it’s actually a handy trick that I use semifrequently
That one’s actually really easy to prove numerically.
Not going to type out a full proof here, but here’s an example.
Let’s look at a two digit number for simplicity. You can write any two digit number as 10*a+b, where a and b are the first and second digits respectively.
E.g. 72 is 10 * 7 + 2. And 10 is just 9+1, so in this case it becomes 72=(9 * 7)+7+2
We know 9 * 7 is divisible by 3 as it’s just 3 * 3 * 7. Then if the number we add on (7 and 2) also sum to a multiple of 3, then we know the entire number is a multiple of 3.
You can then extend that to larger numbers as 100 is 99+1 and 99 is divisible by 3, and so on.
Waaaait a second.
Does that hold for every base, where the divisor is 1 less than the base?
Specifically hexidecimal - could it be that 5 and 3 have the same “sum digits, get divisibility” property, since 15 (=3*5) is one less than the base number 16?
Like 2D16 is16*2+13 = 45, which is divisible by 3 and 5.
Can I make this into a party trick?! “Give me a number in hexidecimal, and I’ll tell you if it’s divisible by 10.”
Am thinking it’s 2 steps:
- Does it end with a 0, 2, 4, 6, 8, A, C, E? Yes means divisible by 2.
- Do the digits add up to a multiple of 5 (ok to subtract 5 liberally while adding)? Skip A and F. For B add 1; C->2, D->3, E->4. If the sum is divisible by 5, then original number is too.
So if 1 and 2 are “yes”, it’s divisible by 10.
E.g.
- DEADBAE16 (=23349547010): (1) ends with E, ok. (2) 3+4+3+1+4=15, divisible by 5. Both are true so yes, divisible by 10.
- C4744416 (=1287482010): (1) ends with 4, ok. (2) 2+4+7+4+4+4=25, ok.
- BEEFFACE16 (=3203398350): (1) E, ok. (2) 1+4+4+2+4=15, ok.
Is this actually true? Have I found a new party trick for myself? How would I even know if this is correct?
How would I even know if this is correct?
You’re gonna have to go to a lot of parties
All numbers are dividible by 3. Just saying.
The utility of Laplace transforms in regards to differential systems.
In engineering school you learn to analyze passive DC circuits early on using not much more than ohms law and Thevenin’s Theoram. This shit can be taught to elementary schoolers.
Then a little while later, you learn how to do non-finear differential equations to help work complex systems, whether it’s electrical, mechanical, thermal, hydrolic, etc. This shit is no walk in the park.
Then Laplace transforms/identities come along and let you turn non-linear problems in time-based space, into much simpler problems in frequency-based space. Shit blows your mind.
THEN a mafacka comes along and teaches you that these tools can be used to turn complex differential system problems (electrical, mechanical, thermal, hydrolic, etc) into simple DC circuits you can analyze/solve in frequency-based space, then convert back into time-based space for the answers.
I know this is super applied calculus shit, but I always love that sweet spot where all the high-concept math finally hits the pavement.
And then they tell you that the fundamental equations for thermal, fluid, electrical and mechanical are all basically the same when you are looking at the whole Laplace thing. It’s all the same…
ABSOLUTELY. I just recently capped off the Diff Eq, Signals, and Controls courses for my undergrad, and truly by the end you feel like a fucking wizard. It’s crazy how much problem-solving/system modeling power there is in such a (relatively) simple, easy to apply, and beautifully elegant mathematical tool.
e^(pi i) = -1
like, what?
3Blue 1Brown actually explains that one in a way that makes it seem less coincidental and black magic. Totally worth a watch
If you think of complex numbers in their polar form, everything is much simpler. If you know basic calculus, it can be intuitive.
Instead of z = + iy, write z = (r, t) where r is the distance from the origin and t is the angle from the positive x-axis. Now addition is trickier to write, but multiplication is simple: (a,b) * (c,d) = (ab, b + d). That is, the lengths multiply and the angles add. Multiplication by a number (1, t) simply adds t to the angle. That is, multiplying a point by (1, t) is the same as rotating it counterclockwise about the origin by an angle t.
The function f(t) = (1, t) then parameterizes a circular motion with a constant radial velocity t. The tangential velocity of a circular motion is perpendicular to the current position, and so the derivative of our function is a constant 90 degree multiple of itself. In radians, that means f’(t) = (1, pi/2)f(t). And now we have one of the simplest differential equations whose solution can only be f(t) = k * e^(t* (1, pi/2)) = ke^(it) for some k. Given f(0) = 1, we have k = 1.
All that said, we now know that f(t) = e^(it) is a circular motion passing through f(0) = 1 with a rate of 1 radian per unit time, and e^(i pi) is halfway through a full rotation, which is -1.
If you don’t know calculus, then consider the relationship between exponentiation and multiplication. We learn that when you take an interest rate of a fixed annual percent r and compound it n times a year, as you compound more and more frequently (i.e. as n gets larger and larger), the formula turns from multiplication (P(1+r/n)^(nt)) to exponentiation (Pe^(rt)). Thus, exponentiation is like a continuous series of tiny multiplications. Since, geometrically speaking, multiplying by a complex number (z, z^(2), z^(3), …) causes us to rotate by a fixed amount each time, then complex exponentiation by a continuous real variable (z^t for t in [0,1]) causes us to rotate continuously over time. Now the precise nature of the numbers e and pi here might not be apparent, but that is the intuition behind why I say e^(it) draws a circular motion, and hopefully it’s believable that e^(i pi) = -1.
All explanations will tend to have an algebraic component (the exponential and the number e arise from an algebraic relationship in a fundamental geometric equation) and a geometric component (the number pi and its relationship to circles). The previous explanations are somewhat more geometric in nature. Here is a more algebraic one.
The real-valued function e^(x) arises naturally in many contexts. It’s natural to wonder if it can be extended to the complex plane, and how. To tackle this, we can fall back on a tool we often use to calculate values of smooth functions, which is the Taylor series. Knowing that the derivative of e^(x) is itself immediately tells us that e^(x) = 1 + x + x^(2)/2! + x^(3)/3! + …, and now can simply plug in a complex value for x and see what happens (although we don’t yet know if the result is even well-defined.)
Let x = iy be a purely imaginary number, where y is a real number. Then substitution gives e^x = e^(iy) = 1 + iy + i(2)y(2)/2! + i(3)y(3)/3! + …, and of course since i^(2) = -1, this can be simplified:
e^(iy) = 1 + iy - y^(2)/2! - iy^(3)/3! + y^(4)/4! + iy^(5)/5! - y^(6)/6! + …
So we’re alternating between real/imaginary and positive/negative. Let’s factor it into a real and imaginary component: e^(iy) = a + bi, where
a = 1 - y^(2)/2! + y^(4)/4! - y^(6)/6! + …
b = y - y^(3)/3! + y^(5)/5! - y^(7)/7! + …
And here’s the kicker: from our prolific experience with calculus of the real numbers, we instantly recognize these as the Taylor series a = cos(y) and b = sin(y), and thus conclude that if anything, e^(iy) = a + bi = cos(y) + i sin(y). Finally, we have e^(i pi) = cos(pi) + i sin(pi) = -1.
Damn that’s actually pretty simple way to use differential equations to show this.
Edit. The series one is also pretty simple.
Multiply 9 times any number and it always “reduces” back down to 9 (add up the individual numbers in the result)
For example: 9 x 872 = 7848, so you take 7848 and split it into 7 + 8 + 4 + 8 = 27, then do it again 2 + 7 = 9 and we’re back to 9
It can be a huge number and it still works:
9 x 987345734 = 8886111606
8+8+8+6+1+1+1+6+0+6 = 45
4+5 = 9
Also here’s a cool video about some more mind blowing math facts
I suspect this holds true to any base x numbering where you take the highest valued digit and multiply it by any number. Try it with base 2 (1), 4 (3), 16 (F) or whatever.
11 X 11 = 121
111 X 111 = 12321
1111 X 1111 = 1234321
11111 X 11111 = 123454321
111111 X 1111111 = 12345654321
You could include 1 x 1 = 1
But thats so cool. Maths is crazy.
Amazing in deed!
Just a small typo in the very last factor
1111111.holt shit
deleted by creator
maybe this will make more sense when I watch the veritasium video, but I don’t have time to do that until the weekend. How is 3x+1 unprovable? won’t all odd numbers multiplied by 3 still be odd? and won’t adding 1 to an odd number always make it even? and aren’t all even numbers by definition divisible by 2? I’m struggling to see how there could be any uncertainty in this
deleted by creator
Just after going through a few examples in my head, the difficulty becomes somewhat more apparent. let’s start with 3. This is odd, so 3(3)+1 = 10. 10 is even so we have 10/2=5.
By this point my intuition tells me that we don’t have a very obvious pattern that we can use to decide whether the function will output 4, 2, or 1 by recursively applying the function to its own output, other than the fact that every other number that we try appears to result in this pattern. We could possibly reduce the problem to whether we can guess that the function will eventually output a power of 2, but that doesn’t sound to me like it makes things much easier.
If I had no idea whether a proof existed, I would guess that it may, but that it is non-trivial. Or at least my college math courses did not prepare me to find one. Since it looks like plenty of professional mathematicians have struggled with it, I have no doubt that if a proof exists it is non-trivial.
The unproven part is that it eventually will reach 1, not that it’s not possible to do the computation. Someone may find a number loop that doesn’t eventually reach 1.
The Fourier series. Musicians may not know about it, but everything music related, even harmony, boils down to this.
Fourier transformed everything
Quickly a game of chess becomes a never ever played game of chess before.
Related: every time you shuffle a deck of cards you get a sequence that has never happened before. The chance of getting a sequence that has occurred is stupidly small.
Most of the time, but only as long as the shuffle is actually random. A perfect riffle shuffle on a brand new deck will get you the same result every time, and 8 perfect riffles on a row get you back to where you started.
I’m guessing this is more pronounced at lower levels. At high level chess, I often hear commentators comparing the moves to their database of games, and it often takes 20-30 moves before they declare that they have now reached a position which has never been reached in a professional game. The high level players have been grinding openings and their counters and the counters to the counters so deeply that a lot of the initial moves can be pretty common.
Also, high levels means that games are narrowing more towards the “perfect” moves, meaning that repetition from existing games are more likely.
Oh yes I agree totally!
At those (insane) levels “everyone” knows the “best” move after the choice of opening and for a long time.
But for the millions of games played every day, I guess it’s a bit less :-)
Euler’s identity, which elegantly unites some of the most fundamental constants in a single equation:
e^(iπ)+1=0
Euler’s identity is often cited as an example of deep mathematical beauty. Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π (π = 3.1415…), the fundamental circle constant.
- The number e (e = 2.718…), also known as Euler’s number, which occurs widely in mathematical analysis.
- The number i, the imaginary unit of the complex numbers.
Furthermore, the equation is given in the form of an expression set equal to zero, which is common practice in several areas of mathematics.
Stanford University mathematics professor Keith Devlin has said, “like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler’s equation reaches down into the very depths of existence”. And Paul Nahin, a professor emeritus at the University of New Hampshire, who has written a book dedicated to Euler’s formula and its applications in Fourier analysis, describes Euler’s identity as being “of exquisite beauty”.
Mathematics writer Constance Reid has opined that Euler’s identity is “the most famous formula in all mathematics”. And Benjamin Peirce, a 19th-century American philosopher, mathematician, and professor at Harvard University, after proving Euler’s identity during a lecture, stated that the identity “is absolutely paradoxical; we cannot understand it, and we don’t know what it means, but we have proved it, and therefore we know it must be the truth”.
This is the one that made me say out loud, “math is fucking weird”
I started trying to read the explanations, and it just got more and more complicated. I minored in math. But the stuff I learned seems trivial by comparison. I have a friend who is about a year away from getting his PhD in math. I don’t even understand what he’s saying when he talks about math.
Recall the existence and uniqueness theorem(s) for initial value problems. With this, we conclude that e^(kx) is the unique function f such that f’(x) = k f(x) and f(0) = 1. Similarly, any solution to f’’ = -k^(2)f has the form f(x) = acos(kx) + bsin(kx). Now consider e^(ix). Differentiating it is the same as multiplying by i, so differentiating twice is the same as multiplying by i^(2) = -1. In other words, e^(ix) is a solution to f’’ = -f. Therefore, e^(ix) = a cos(x) + b sin(x) for some a, b. Plugging in x = 0 tells us a = 1. Differentiating both sides and plugging in x = 0 again tells us b = i. So e^(ix) = cos(x) + i sin(x).
We take for granted that the basic rules of calculus work for complex numbers: the chain rule, and the derivative of the exponential function, and the existence/uniqueness theorem, and so on. But these are all proved in much the same way as for real numbers, there’s nothing special behind the scenes.
Time for a deep dive. Wish me luck, lads.
Let us know what you find in the depths.
The one I bumped into recently: the Coastline Paradox
“The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve–like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension.”




















